问题:我需要确定一个低电阻传感器的电阻变化,我的计划只是在细线传感器引线上施加一个已知的电压,然后测量电流。然后通过欧姆定律(电阻=电压/电流或R=V/I),我可以很容易地计算传感器电阻。但是,传感器引线的标称电阻和温度系数会影响读数从而导致我无法校准的错误。该怎么办?
解决方案:使用开尔文电桥来解决这个常见的问题。为此,使用电流源通过现有导线向传感器提供已知电流。然后在传感器上增加另外两条引线,通过高阻抗表或缓冲放大器读取传感器上的电压(图1)。再次使用欧姆定律,但使用已知电流和测量电压。在这种四线制结构下,以两条非临界电压传感线,传感器引线的电阻不会进入方程中。
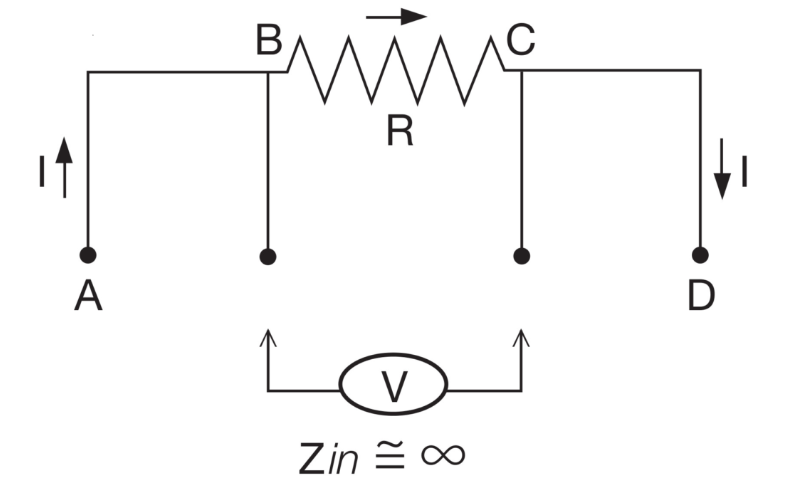
图1:为了解决传感器引线中的电阻影响测量精度的问题,使用四线开尔文排列,将已知电流从A到D穿过传感器R,然后使用高阻抗计或缓冲放大器通过两个附加导线在B-C处读取传感器上的电压。
为了尽量减少传感器的自发热和可能的错误,在传感器上提供足够电压的同时,使用尽可能低的电流。在大多数情况下,传感器上的最大电压将在1到10 V之间。
注意,这种技术的一种变化通常用于测量负载(如电机)的电流,使用与负载串联的低值感测电阻器(图2)。对于负载电流感测,您使用一个已知的电阻,通常为一欧姆或更小,通常在毫欧姆范围内。然后使用差分缓冲放大器(可能需要与电路的其余部分进行电气隔离)测量其两端的电压,并再次使用欧姆定律,但这次I=V/R。
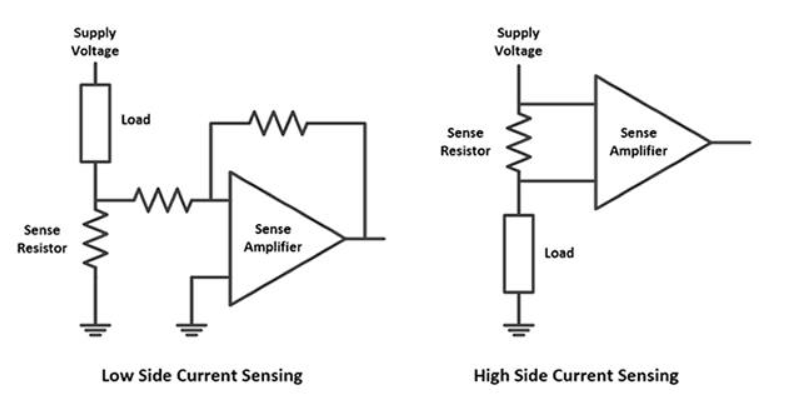
在负载侧和负载之间使用电阻来测量负载。
开尔文4线技术证明工程师如何使用巧妙的拓扑结构来克服误差源,而不是试图使事情变得完美(在这里,传感器引线的电阻为零)。相反,工程师们开发出方法让误差源“退出”方程。另一个很好的例子是比例测量设计,例如惠斯通电桥,它使用电阻比而不是绝对电阻值。






 客服微信
客服微信 查ic网订阅号
查ic网订阅号

